- Profile
- さいらいじ・ふみお 1992年大阪大学理学部数学科卒。2000年同大学院理学研究科数学専攻博士課程単位取得退学。姫路の賢明女子学院中学校・高等学校教諭を経て、2002年広島国際大学社会環境科学部建築創造学科講師。2006年同助教授。2007年工学部建築学科准教授。2013年工学部住環境デザイン学科教授。2017年4月から現職。これまで中央大学、広島大学非常勤講師も兼任。博士(理学)。広島県出身。
天才数学者たちを魅了した数の宇宙
地中で13年とか17年過ごし地上に出てくる「素数ゼミ」がアメリカに生息しています。13も17も素数で、他のセミと羽化が重なる周期(最小公倍数)が大きく、他のセミと交雑する機会が少なかったため絶滅しなかったと考えられています。また現代ではインターネットの情報の暗号化に素数は欠かせないものです。自然も人間も意外なところで素数の恩恵を受けています。ドイツの天才数学者ガウスは、数の性質を研究する整数論を「数学の女王」と言いましたが、素数はその整数論の中心テーマです。整数論を専門とする数学者の西来路文朗広島国際大看護学科教授は、素数をテーマにした著書(清水健一氏との共著)を科学啓蒙新書ブルーバックス(講談社)から一昨年と今年立て続けに2冊出版しました。数の基本であるのに今なお究め尽くせぬ神秘に満ちた素数の魅力について、西来路教授に聞きました。

自然数の中で素数(太字)は無秩序に現れるように見える
2300年前に証明された無限性
1より大きな自然数のうち1とその数自身以外で割り切れない数が素数です。1より大きなすべての自然数は素数の積に分解できます。つまり物質が原子から成り立っているように、自然数は素数から成り立っています。2300年近くも前のギリシャ時代に、ユークリッド(B.C.330-275頃) は『原論』の中で、素数が無限にあることを証明しています。その有名な証明のアイデアは、与えられた素数から、それらと異なる新しい素数を作ることでした。ちなみに『原論』は定義、命題、証明という今の数学のスタイルを作った本です。

自然数は素数でできていて、その素数が無限に存在することはこんな昔から分かっていました。しかし、一見単純そうな素数なのに、n番目の素数をnで表す式はいまだに見つかっていません。自然数の中で規則的に素数が現れるわけではないのです。ここから「素数分布」という問題が生じてきます。素数がどのように存在しているかは謎に満ちていて、とても深遠な数の宇宙に私たちを導いていきます。
不思議な現象が次々と
その魅力を紹介するために2015年の『素数が奏でる物語』に続いて今年は『素数はめぐる』を出版しました。1冊目は「4n+1」(4で割って1余る)型と「4n+3」(4で割って3余る)型に素数を分類、2つの等差数列を手掛かりに、多くの天才数学者たちを魅了した世界を紹介しました。例えば、

というように、2つの型の素数で性質が全く異なるのです。これらの現象の背後にはガウス整数a+bi(a、b:整数)という数の世界の素因数分解の法則が横たわっています。
2冊目の本「素数はめぐる」では「1÷素数」が生み出す驚きに満ちた循環小数をテーマに数論の世界を紹介しました。「1÷7」は小数では「0.142857142857142857 …」という循環小数になります。この循環する部分「142857」は「ダイヤル数」と呼ばれ、これに1、2、3、4、5、6を順にかけると「142857」「285714」「428571」「571428」「714285」「857142」とダイヤルのように「142857」を巡回させる6通りの数字が現れます。またこの6通りの数字を「142+857」「285+714」のように2等分して足すとすべてが「999」になります。これと同じような不思議な現象には「1÷17」「1÷19」「1÷23」「1÷29」でも出会えます。
素数研究が新しい数学の分野の源泉に
素数は「自然数の原子」であり根源的です。したがって、素数の性質を追究することで多様な数学が広がっていきます。上流で川の流れを変えた方が下流で変えるより変化が大きいのに似ています。
例えば、フェルマー(1607-1665)は、pが素数の時、ap-aがpで割り切れることを示しました。p=5として説明すると、1の5乗は1で1を引くと0になります。2の5乗は32で2を引くと30になります。3の5乗は243で3を引くと240になります。0も30も240も5で割り切れます。このようにa5-aは5で割り切れます。
この性質は「フェルマーの小定理」と呼ばれています。規則性は美しいが、何の意味があるのか、と思われるかもしれません。この性質の背後には、整数を素数pで割った余りの数0、1、…、p-1たちが、有理数と同じような四則演算を持っている、という事実があります。それぞれの素数ごとに有限体と呼ばれる新しい数の世界が広がっているのです。
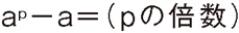
オイラー(1707-1783)はユークリッドが示した素数の無限性に新しい証明を与えました。オイラーは素数の逆数の和が発散することを示しました。素数が有限個なら逆数の和は収束しますので、逆数の和が発散することから素数が無限個あることが分かります。オイラーの証明は、複素数も含めた関数の微積分を用いる解析的数論につながっていきました。
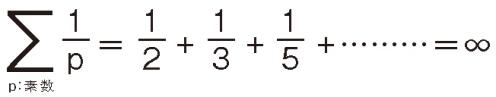
ガウス(1777-1855)は、素数の間に「平方剰余の相互法則」と呼ばれる法則性があることを証明しました。2つの奇数の素数p、q に対して、「x2-p (x : 整数) の素因数にq が現れる」と「x2-q (x: 整数)の素因数にp が現れる」のはほぼ同じ、という法則です。例えば、x2-5の素因数には、x=4のとき、42-5=11が現れます。一方、x2-11 の素因数にも、x=1のとき、12-11=-10=-2×5と5 が現れます。この法則は抽象的で意味が分かりにくいと思いますが、ガウスは「黄金定理」と呼んで7通りの証明をつけています。その証明ごとに新しい数学が発展したと言っても過言ではなく、まさに黄金の鉱脈です。素数は古代ギリシャ時代以降よく研究されている対象ですが、分からないことが数多くあります。身近に未解決の問題があること、不思議な現象があること、その現象を追究することで新しい数学の世界が広がっていくことが素数の魅力なのです。
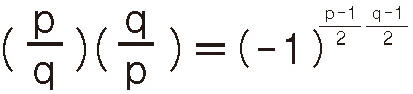
双子素数研究で大きな成果
最近の話題では双子素数があります。 (3、5)、(5、7)、(11、13)のように差が2の連続する素数の組を双子素数といいます。双子素数は無数にあるかどうかも分かっていませんが、最近、この問題に大きな進展がありました。2013年、中国生まれのジャンという数学者が、連続する素数の組で差が7000万以下のものが無数に存在する、という定理を示しました。差がある値以下の連続する素数の組が無数にあることを示した点が画期的です。その後、定理は改良され、現在では差が246以下である連続する素数の組が無数に存在することまで示されています。いつかこの差が2になれば、双子素数の無限性が証明されたことになります。
また、コンピューターの登場で、近年大きい素数を見つけやすくなりました。例えば、1876 年にリュカが手計算で12 番目のメルセンヌ素数(2n-1の形の素数)、39 桁を発見しています。1952年にロビンソンがコンピューターを使って、13番目のメルセンヌ素数157桁を発見し、現在はクーパーの22,338,618桁が最大です。このように素数研究は日々進化しています。
私が現在研究しているp進数も素数から導かれる世界です。p進数は1897年にドイツのヘンゼルが考案した実数とは異なる新しい数です。p進数の世界で「形式群のpn等分方程式の解の性質(ガロワ群)」を研究しています。
素数の引き起こす世界の法則性の美しさと深みが、私をとらえて放しません。

ブルーバックスの2冊と近刊の数論入門書を手に





 前の記事へ
前の記事へ








